Back to Courses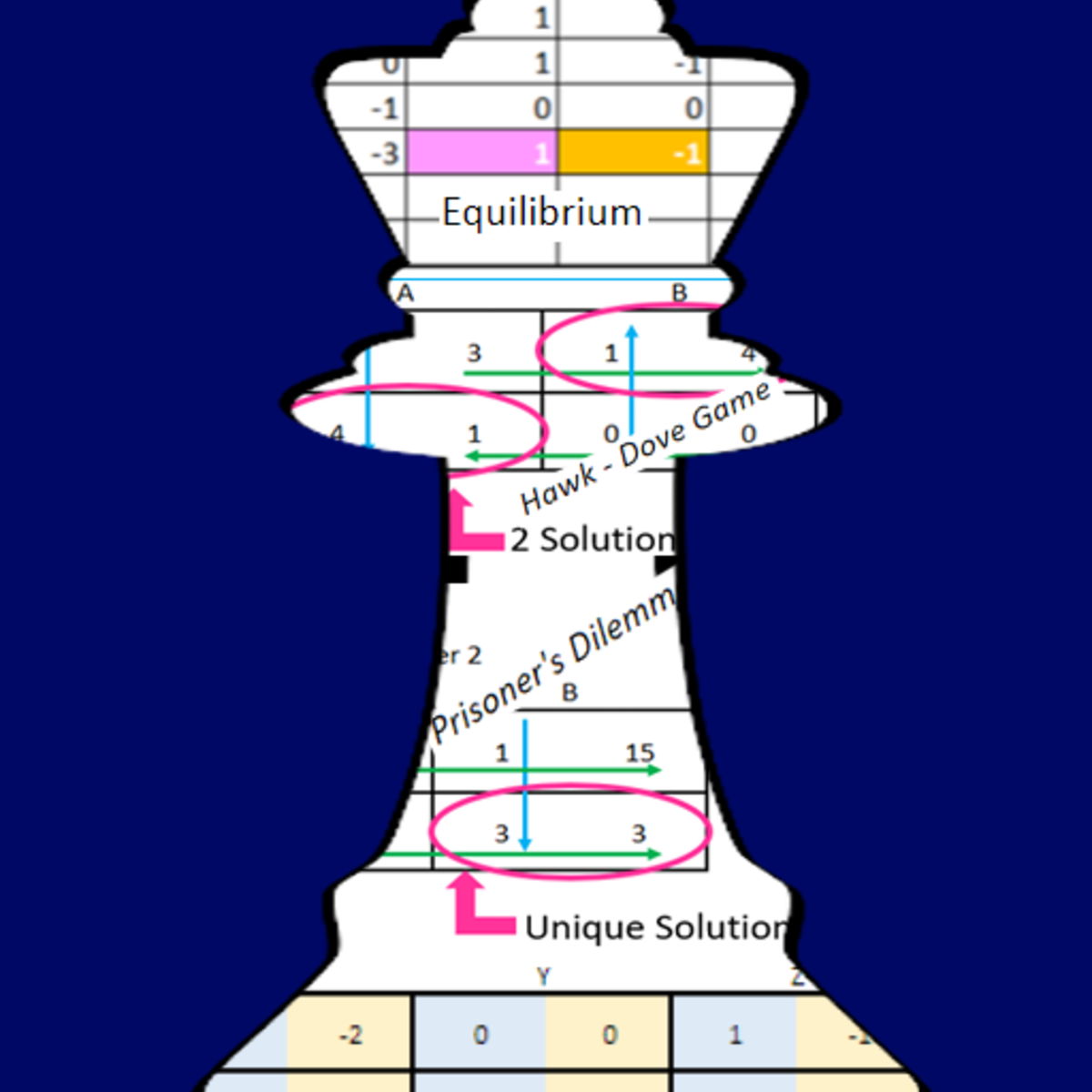






Math And Logic Courses - Page 13
Showing results 121-130 of 148

Game-Theoretic Solution Concept with Spreadsheets
In this 2-hour long project-based course, you will learn how to use 2 Game-theoretic decision rules: Maximin strategy, Minimax strategy, and the solution concept, Nash Equilibrium. You will be familiarized with key terminologies in Game Theory and learn the underlying computation mechanism of each method to solve problems. Also, you will be solving higher order payoff matrices using custom spreadsheet based solution template (one for each method) and learn to interpret the results.
Note: This course works best for learners who are based in the North America region. We’re currently working on providing the same experience in other regions.

Information Theory
The lectures of this course are based on the first 11 chapters of Prof. Raymond Yeung’s textbook entitled Information Theory and Network Coding (Springer 2008). This book and its predecessor, A First Course in Information Theory (Kluwer 2002, essentially the first edition of the 2008 book), have been adopted by over 60 universities around the world as either a textbook or reference text.
At the completion of this course, the student should be able to:
1) Demonstrate knowledge and understanding of the fundamentals of information theory.
2) Appreciate the notion of fundamental limits in communication systems and more generally all systems.
3) Develop deeper understanding of communication systems.
4) Apply the concepts of information theory to various disciplines in information science.

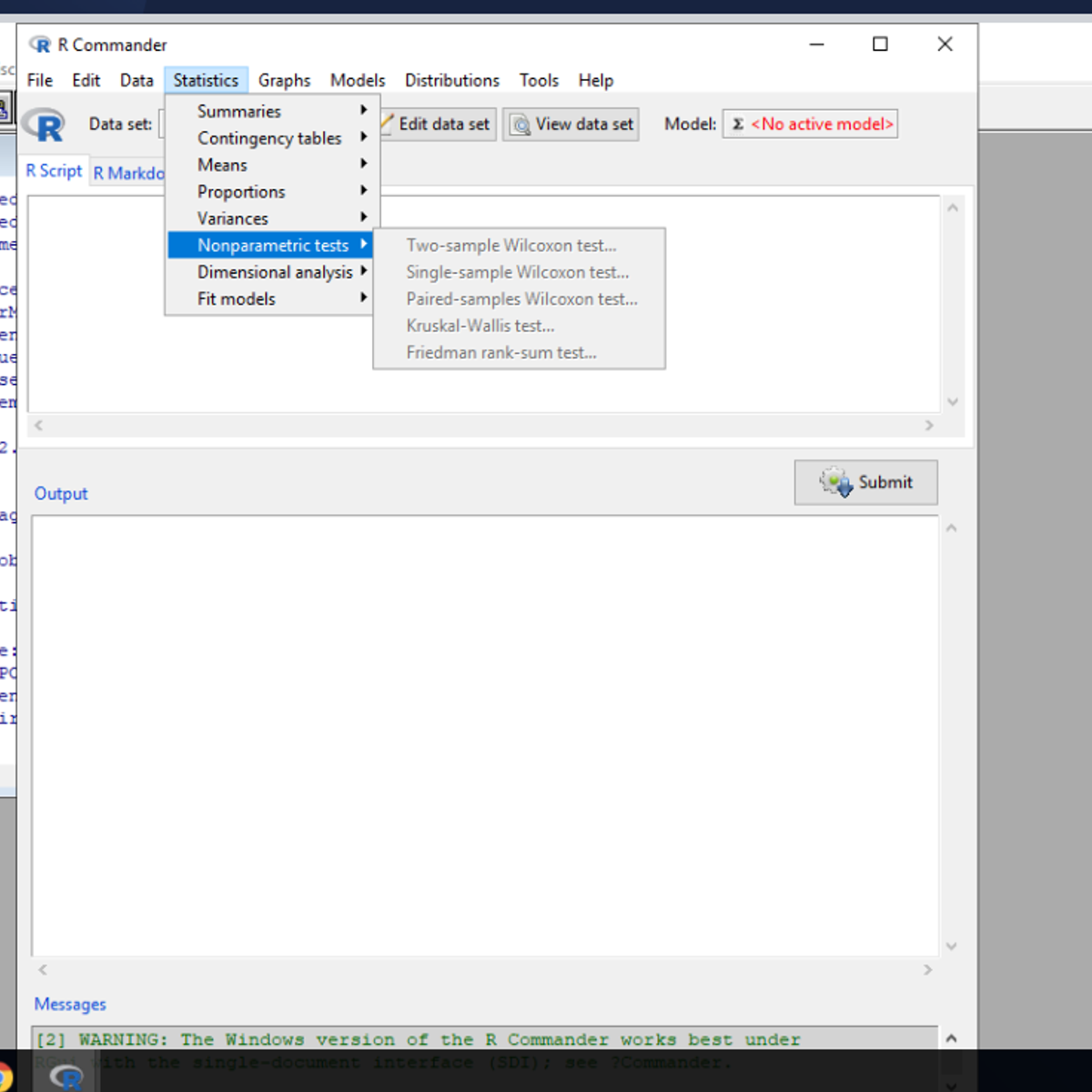
Non parametric Tests using R Cmdr
In this project , you will learn how to conduct non parametric tests using Rcmdr. Non parametric tests are powerful tests which are conducted when underlying assumptions are not met in the data . After completing the project, you will be able to apply the appropriate test for the right data set. You will also learn how to do it in an easy to use Rcmdr.

Calculus through Data & Modelling: Series and Integration
This course continues your study of calculus by introducing the notions of series, sequences, and integration. These foundational tools allow us to develop the theory and applications of the second major tool of calculus: the integral. Rather than measure rates of change, the integral provides a means for measuring the accumulation of a quantity over some interval of input values. This notion of accumulation can be applied to different quantities, including money, populations, weight, area, volume, and air pollutants. The concepts in this course apply to many other disciplines outside of traditional mathematics. Through projects, we will apply the tools of this course to analyze and model real world data, and from that analysis give critiques of policy.
Following the pattern as with derivatives, several important methods for calculating accumulation are developed. Our course begins with the study of the deep and significant result of the Fundamental Theorem of Calculus, which develops the relationship between the operations of differentiation and integration. If you are interested in learning more advanced mathematics, this course is the right course for you.
Greedy Algorithms, Minimum Spanning Trees, and Dynamic Programming
The primary topics in this part of the specialization are: greedy algorithms (scheduling, minimum spanning trees, clustering, Huffman codes) and dynamic programming (knapsack, sequence alignment, optimal search trees).

Algebra: Elementary to Advanced - Functions & Applications
After completing this course, students will learn how to successfully apply functions to model different data and real world occurrences. This course reviews the concept of a function and then provide multiple examples of common and uncommon types of functions used in a variety of disciplines. Formulas, domains, ranges, graphs, intercepts, and fundamental behavior are all analyzed using both algebraic and analytic techniques. From this core set of functions, new functions are created by arithmetic operations and function composition. These functions are then applied to solve real world problems. The ability to picture many different types of functions will help students learn how and when to apply these functions, as well as give students the geometric intuition to understand the algebraic techniques. The skills and objectives from this course improve problem solving abilities.

Introduction to C++ Programming: Build a Calculator
By the end of this project, you will be able to create a simple calculator as well as an advanced one, which will be achieved by learning the basic concepts of C++ such as variables, DataTypes, if conditions, and more programming concepts. By applying these concepts you can also create programs that users can interact with. These programming concepts can also be applied using other Programming Languages such as Java and Python, not just C++.
Note: This course works best for learners who are based in the North America region. We’re currently working on providing the same experience in other regions.

The Data Scientist’s Toolbox
In this course you will get an introduction to the main tools and ideas in the data scientist's toolbox. The course gives an overview of the data, questions, and tools that data analysts and data scientists work with. There are two components to this course. The first is a conceptual introduction to the ideas behind turning data into actionable knowledge. The second is a practical introduction to the tools that will be used in the program like version control, markdown, git, GitHub, R, and RStudio.

Vector Calculus for Engineers
This course covers both the basic theory and applications of Vector Calculus. In the first week we learn about scalar and vector fields, in the second week about differentiating fields, in the third week about multidimensional integration and curvilinear coordinate systems. The fourth week covers line and surface integrals, and the fifth week covers the fundamental theorems of vector calculus, including the gradient theorem, the divergence theorem and Stokes’ theorem. These theorems are needed in core engineering subjects such as Electromagnetism and Fluid Mechanics.
Instead of Vector Calculus, some universities might call this course Multivariable or Multivariate Calculus or Calculus 3. Two semesters of single variable calculus (differentiation and integration) are a prerequisite.
The course contains 53 short lecture videos, with a few problems to solve following each lecture. And after each substantial topic, there is a short practice quiz. Solutions to the problems and practice quizzes can be found in instructor-provided lecture notes. There are a total of five weeks to the course, and at the end of each week there is an assessed quiz.
Download the lecture notes:
http://www.math.ust.hk/~machas/vector-calculus-for-engineers.pdf
Watch the promotional video:
https://youtu.be/qUseabHb6Vk

Problem Solving Using Computational Thinking
Have you ever heard that computers "think"? Believe it or not, computers really do not think. Instead, they do exactly what we tell them to do. Programming is, "telling the computer what to do and how to do it."
Before you can think about programming a computer, you need to work out exactly what it is you want to tell the computer to do. Thinking through problems this way is Computational Thinking. Computational Thinking allows us to take complex problems, understand what the problem is, and develop solutions. We can present these solutions in a way that both computers and people can understand.
The course includes an introduction to computational thinking and a broad definition of each concept, a series of real-world cases that illustrate how computational thinking can be used to solve complex problems, and a student project that asks you to apply what they are learning about Computational Thinking in a real-world situation. This project will be completed in stages (and milestones) and will also include a final disaster response plan you'll share with other learners like you.
This course is designed for anyone who is just beginning programming, is thinking about programming or simply wants to understand a new way of thinking about problems critically. No prior programming is needed. The examples in this course may feel particularly relevant to a High School audience and were designed to be understandable by anyone.
You will learn:
-To define Computational Thinking components including abstraction, problem identification, decomposition, pattern recognition, algorithms, and evaluating solutions
-To recognize Computational Thinking concepts in practice through a series of real-world case examples
-To develop solutions through the application of Computational Thinking concepts to real world problems
Popular Internships and Jobs by Categories
Find Jobs & Internships
Browse
© 2024 BoostGrad | All rights reserved